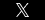Law Department Management Blog
I wrote about the article by Bill Turner of Womble Carlyle on Monte Carlo simulations, and emailed him with some questions (See my post of June 26, 2009: Monte Carlo and sensitivity analysis.). One was about law departments that have used the firm’s Monte Carlo capabilities. While unwilling to disclose the name of a specific law department that has used the software, “we have used this tool to develop value-driven alternative engagements for some clients.”
Turner also wrote clearly about multivariate regression. “In multivariate regression, you’re often testing to see how much of a variable, X, contributed to the forecast Y, and whether X is significant in the model, overall. The Monte Carlo tools perform sensitivity analysis by creating rank correlation coefficients between the assumptions and the model forecasts while the simulation is running. These coefficients indicate the strength with which the assumptions and the forecasts change together. The coefficients are squared and normalized to 100%.
One of the key differences between using these techniques vs. multivariate regression is that multivariate regression analysis is usually run against actual data (where variables are then tested for significance, multicolliniarity, heteroskedasticity, auto correlation, etc.) whereas Monte Carlo analysis creates the data (and then runs the sensitivity) based on defined parameters. In principle, the concepts are similar, though the sensitivity analysis demonstrated in the paper involves how much the model assumptions contributed to the variation in the forecast rather than how much the assumptions contributed to the forecast itself. The goal is to measure risk.”
(See my post of Dec. 31, 2008: regression statistics with 6 references.).
Thank you very much, Bill!